Answer:
A) The graph passes through the point (0, 3), and for each increase of 1 in the x-values, the y-values increase by 1.8
Explanation:
We are given the function,
 .
.
First, we will substitute x= 0 in the function.
So, we get,
 implies
implies
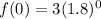 i.e. f(0)= 3
i.e. f(0)= 3
Thus, the graph of the function passes through the point (0,3).
Also, we get the table of the values as,
x
 Difference in f(x) values
Difference in f(x) values
1
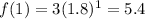 9.72-5.4 = 4.32
9.72-5.4 = 4.32
2
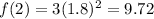 17.496 -9.72= 7.776
17.496 -9.72= 7.776
3
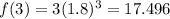 1.4928-17.496=13.997
1.4928-17.496=13.997
4
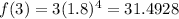
As, we have,
The factor of increase in the y-values =
 =
=
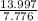 = 1.8
= 1.8
Thus, we get, the correct option is,
A)The graph passes through the point (0, 3), and for each increase of 1 in the x-values, the y-values increase by 1.8