Question

Complete the following proof related to the figure below.

Given: bisects RT = ST

Prove:


Which of the following would be the reason for line 4 in the proof?

SSS

ASA

SAS

Answer 1

the answer is SSS man

Answer 2

Answer: SSS

Explanation:

In the picture, we are given:
`\overline{TQ}\text{ bisects }\overline{RS}`

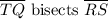
RT=ST

Now, in ΔRTQ and ΔSTQ, we have

RT=ST

RQ=SQ [Definition of bisector of segment]

TQ=TQ [Reflexive property]

By SSS property of congruence, we have

ΔRTQ ≅ΔSTQ

• SSS property of congruence tells that if all three sides in a triangle have the same length as the corresponding sides in the other triangle then the triangles are said to be congruent.