Answer:
PS=
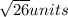
Explanation:
Given : PQRS is a trapezoid on a coordinate plane P(7,4) Q(10,4) R(13,-1) S(8,-1).
To find:: Length of the side PS
Solution : Using the distance formula, we can find the length of the side PS, therefore
PS=

PS=

PS=
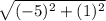
PS=
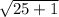
PS=
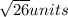
which is the required length of the side PS.