Question

Please help me with the fraction problems please. It's linear inequalities.

I need help with 3, 7, 8, and 12

Answer 1

3.
`\frac{9x+1}4>2x-1`

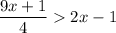
Multiply both sides by 4:

`4*\frac{9x+1}4>4*(2x-1)\implies9x+1>8x-4`

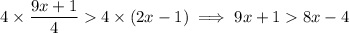
Subtract
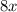`8x` and 1 from both sides:

`9x+1-8x-1>8x-4-8x-1\implies x>-5`

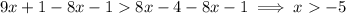
7.
`\frac x3-1<\frac x2+3`

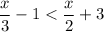
Multiply both sides by 6; this choice is motivated by the fact that
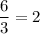`\frac63=2` and
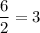`\frac62=3`. In other words, 6 is the least common multiple of 3 and 2, which allows us to eliminate the denominators of the fractions in this inequality.

`6\left(\frac x3-1\right)<6\left(\frac x2+3\right)\implies2x-6<3x+18`

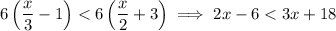
Subtract
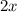`2x` and 18 from both sides:

`2x-6-2x-18<3x+18-2x-18\implies -24<x`

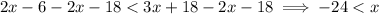
8. Since these are all linear inequalities, I think this is supposed to read

`2x-1>4-\frac12x\iff2x-1>4-\frac x2`

Multiply both sides by 2:

`2(2x-1)>2\left(4-\frac x2\right)\implies4x-2>8-x`

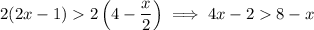
Subtract
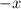`-x` and -2 from both sides:

`4x-2-(-x)-(-2)>8-x-(-x)-(-2)\implies 5x>10`

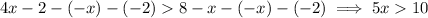
Divide both sides by 5:

`\frac{5x}5>\frac{10}5\implies x>2`

12.
`12\left(\frac14+\fracx3\right)>15`

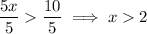
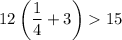
12 is the least common multiple of 4 and 3; distributing it to both terms on the left gives

`\frac{12}4+\frac{12x}3=3+4x`

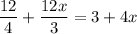
so we have

`3+4x>15`

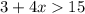
Subtract 3 from both sides:

`3+4x-3>15-3\implies4x>12`

Divide both sides by 4:

`\frac{4x}4>\frac{12}4\implies x>3`