Answer:
a = 7 hours is the time must be allowed to maximize the utility of a typical Marbellite.
Step-by-step explanation:
Note: Some corrections in the questions
Wrong Utility function is = uſm, b, B) = m + 166 – 62 – B/50,
Correct Utility function = u ( m, b, B) = m + 16
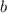 -
-
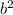 -
-
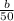
Data Given:
Marbella residents = 101
Utility Function = u ( m, b, B) = m + 16
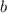 -
-
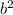 -
-
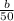
where m = amount of maccaroni (Kg)
b = hours spend on beach
B = total person-hours spent on beach
Each residents has an income of 10$ per day
maccaroni costs = 1$ per kg
Required = How many hours per day should they allow in order to maximize the utility of a typical Marbellite ?
Solution:
In order to find the required statement, we need to find the value of
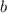 from the utility function.
from the utility function.
And it can be done by applying the partial differentiation on the utility function.
u ( m, b, B) = m + 16
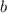 -
-
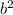 -
-
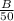
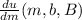 =
=
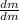 +16
+16
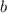 -
-
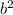 -
-
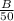
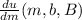 = 1
= 1
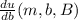 = 1m +16
= 1m +16
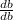 -
-
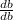
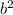 -
-
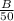
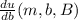 = 16- 2
= 16- 2
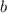
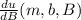 = 1m +16b- 2
= 1m +16b- 2
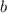 -
-
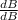
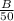
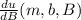 = -
= -
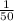
Solving the above equations, we will get b.
b = 7 hours
Hence, a = 7 hours is the time must be allowed to maximize the utility of a typical Marbellite.