Question

The rectangle below has an area of 1 8 x 3 18x 3 square meters and a length of 2 x 2 2x 2 meters.

Answer 1

`\text{The width of rectangle}=9x\text{ meters}`

Explanation:

We have been given that the rectangle has an area of
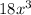`18x^3` square meters and a length of
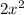`2x^(2)`. We are asked to find the width of rectangle.

Since we know that area of a rectangle is width times length of the rectangle, so we can find width of our given rectangle by dividing given area by length of rectangle.

`\text{Area of rectangle}=\text{Width of rectangle *Length of the rectangle}`

`\frac{\text{Area of rectangle}}{\text{Length of rectangle}}=\frac{\text{Width of rectangle *Length of the rectangle}}{\text{Legth of rectangle}}`

`\text{The width of rectangle}=\frac{\text{Area of rectangle}}{\text{Length of rectangle}}`

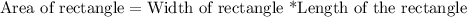
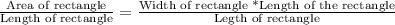
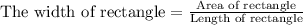
Upon substituting our given values in above formula we will get,

`\text{The width of rectangle}=\frac{18x^3\text{ meter}^2}{2x^2\text{ meters}}`

`\text{The width of rectangle}=\frac{9x^3\text{ meters}}{x^2}`

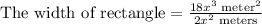
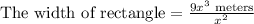
Using exponent rule for quotient
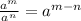`(a^m)/(a^n)=a^(m-n)` we will get,

`\text{The width of rectangle}=9x^(3-2)\text{ meters}`

`\text{The width of rectangle}=9x^(1)\text{ meters}=9x\text{ meters}`

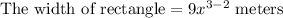
Therefore, width of our given rectangle will be 9x meters.