Answer:
![\sqrt[7]{x^(3) }= x^{(3)/(7) }](https://img.qammunity.org/2022/formulas/mathematics/high-school/9ua4766ul1mkdv481aeeqts5nnxnicunla.png)
Explanation:
In order to solve this question we need to understand the following.
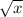 =
=
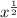
![\sqrt[3]{x} = x^{(1)/(3) }](https://img.qammunity.org/2022/formulas/mathematics/high-school/b29kk0zjfjegj9jictpd3z1ly3vj0bao90.png)
![\sqrt[4]{x}= x^{(1)/(4) }](https://img.qammunity.org/2022/formulas/mathematics/high-school/h9cfruhuz1z86phtuzyj5lt8tihd5t5nb3.png)
(Notice that the numerator of the fraction is the power of the x that is being squared)
If you need proof here it is.....
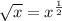
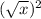 =
=

x = x
Now that we got that out of the way we can rewrite
![\sqrt[7]{x^(3) }](https://img.qammunity.org/2022/formulas/mathematics/high-school/1775omlhvwsc3l5xiwopd7k4pe37v1lf0d.png) as........
as........
![\sqrt[7]{x^(3) }= x^{(3)/(7) }](https://img.qammunity.org/2022/formulas/mathematics/high-school/9ua4766ul1mkdv481aeeqts5nnxnicunla.png)