Rewrite y =
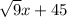
– 2 to make it easy to graph using a translation. Describe the graph.
Rewritten, y =
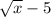
– 2. It is the graph of y =
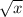
translated 5 units left and 2 units down.
Rewritten, y =
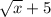
– 2. It is the graph of y =
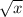
translated 5 units right and 2 units down.
Rewritten, y =
![\sqrt[3]{x} +5](https://img.qammunity.org/2020/formulas/mathematics/high-school/yzzw2geykajie3aogh82iyc3ohx4rrdf.png)
– 2. It is the graph of y =
![\sqrt[3]{x}](https://img.qammunity.org/2020/formulas/mathematics/high-school/adp5h6zbpgyn5rixh96ki4nbf91jilhd94.png)
translated 5 units left and 2 units down.
Rewritten, y =
![\sqrt[3]{x} +5](https://img.qammunity.org/2020/formulas/mathematics/high-school/yzzw2geykajie3aogh82iyc3ohx4rrdf.png)
– 2. It is the graph of y =
![\sqrt[3]{x}](https://img.qammunity.org/2020/formulas/mathematics/high-school/adp5h6zbpgyn5rixh96ki4nbf91jilhd94.png)
translated 5 units right and 2 units down.