Answer:
The length of AC is 222 units.
Explanation:
Given AC and AE are common external tangents of G and D.
BC= 123 , GB=20 and AG=101.
We have to find the measure of AC.
As, a straight line joined from the center i.e radius is perpendicular to tangent drawn. Therefore,
In ΔABG, by Pythagoras theorem
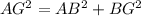
⇒
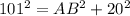
⇒
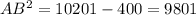
⇒ AB=99 units.
Hence, AC=AB+BC=99+123=222 units.
The length of AC is 222 units.