Question

P;lease helpppp 35 pnts!!!!

In the diagram, diameter AC intersects chord BD at point E such that AE = 2.5 units and DE = 3.4 units. Point O is the center of the circle, and the radius of the circle is 5 units. What is the approximate length of BE? A. 5.5 units B. 4.5 units C. 6.0 units D. 5.0 units

Answer 1

The length of BE is 5.5 units.(A correct option)

Explanation:

Given diameter AC intersects chord BD at point E such that AE = 2.5 units and DE = 3.4 units. Point O is the center of the circle, and the radius of the circle is 5 units. we have to find the approximate length of BE.

CE=CO+OE=5+(OA-AE)=5+2.5=7.5 units.

Now, by Intersecting Chord Theorem which states that when two chords intersect each other inside a circle then the products of their segments are equal.

⇒
`CE* AE=BE* DE`

⇒
`7.5* 2.5=BE* 3.4`

⇒
`BE=(7.5* 2.5)/(3.4)=5.5147\sim5.5units`

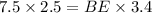
Hence, the length of BE is 5.5 units.