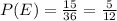Answer:
The probability that the value of the second die is higher than the first
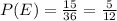
Explanation:
Explanation:-
In a single throw with two dice total number of sums = 6 X 6 = 36
Let 'E' be the event of the second die is higher than the first
Total number of cases
= {( 1,1), (1,2 )( 1,3), (1,4) , (1,5) ,(1,6)
( 2,1), (2,2 )( 2,3), (2,4) , (2,5),(2,6)
( 3,1), (3,2 )( 3,3), (3,4) , (3,5),(3,6)
( 4,1), (4,2 )( 4,3), (4,4) , (4,5),(4,6)
( 5,1), (5,2 )( 5,3), (5,4) , (5,5),(5,6)
( 6,1), (6,2 )( 6,3), (6,4) , (6,5),(6,6)}
The favourable cases
n(E) = {(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)} = 15
The probability that the value of the second die is higher than the first