Answer: The correct option is (D) (4, -6).
Step-by-step explanation: Given that the areas of the triangles ADC and DCB are in the ratio 3 : 4.
We are to find the co-ordinates of point C.
From the diagram, we note that
the co-ordinates of point A and B are A(1, -9) and B(8,-2).
So, the length of the line segment AB, calculated by distance formula, is
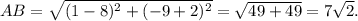
Now, area of ΔADC is
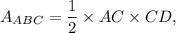
and area of ΔDCB is
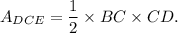
According to the given information, we have
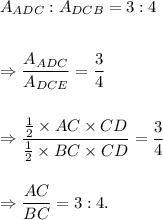
So, the point C divides the line segment AB internally in the ratio 3 : 4.
We know that
if a point divides a line segment with end-points (a, b) and (c, d) internally in the ration m : n, then its co-ordinates are
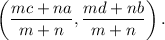
Since point C divides the line segment AB with end-points A(1, -9) and B(8, -2) internally, so the co-ordinates of point C will be
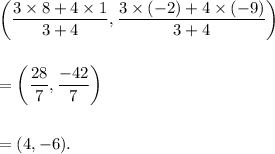
Thus, the co-ordinates of point C are (4, -6).
Option (D) is correct.