Answer:
B (3 - i)
Explanation:
To find the quotient of the complex numbers you must multiply the numerator and the denominator by the conjugate of the denominator
Example: The conjugate of (3 - i) is (3 + i)
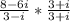
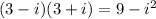
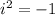
So
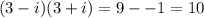
Denominator= 10
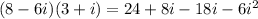
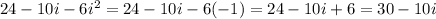
Numerator = 30 - 10i
Then
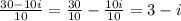
The correct answer is B