To solve this problem we use the general kinetic equations.
We need to know the time it takes for the car to reach 130 meters.
In this way we have to:

Where
 = initial position
= initial position
 = initial velocity
= initial velocity
 = acceleration
= acceleration
 = time
= time
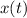 = position as a function of time
= position as a function of time

 .
.
We use the quadratic formula to solve the equation.
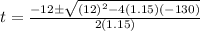
t = 6.63 s and t = -17.1 s
We take the positive solution. This means that the car takes 6.63 s to reach 130 meters.
Then we use the following equation to find the final velocity:

Where:
 = final speed
= final speed

The final speed of the car is 27.25 m/s