Answer: AAS Theorem
Explanation:
In the given figure , we have

By CPCTC [Congruent parts of congruent triangles are congruent], we have
 (1)
(1)
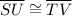 (2)
(2)
Now in
 , we have
, we have
 (From 1)
(From 1)
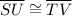 (From 2)
(From 2)
 (Vertical angles)
(Vertical angles)
Therefore by AAS theorem of congruence , we have
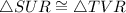
- AAS theorem of congruence says that if two angles and a non-included side of a triangle are congruent to the corresponding parts of other triangle then the triangles are said to be congruent.