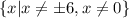Answer:
Option B is correct.
The domain of the function h(x) is:
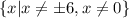
Explanation:
Domain states that the complete set of all the possible values of the independent variable where function is defined.
Given the function:
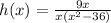
To find the excluded value in the domain of the function.
equate the denominator to 0 and solve for x.
i.e
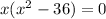
⇒x = 0 and

⇒x = 0 and
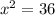
or
x = 0 and

So, the domain of the function h(x) is the set of all real number except x = 0 and

Therefore, the domain of the function h(x) is: