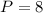Question

A 60-Hz 3-phase induction motor is required to drive a load at approximately 850 rpm. How many poles should the motor have

Answer 1

8 poles

Step-by-step explanation:

Given

`Frequency, f = 60Hz`

`Speed, n_s = 850rpm`

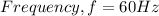
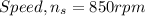
Required

Calculate the number of poles the motor should have?

To solve this question, we make use of synchronous angular velocity formula

`n_s = (120f)/(P)`

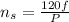
Where

`P = Number\ of\ Poles`

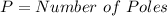
Substitute values for
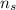`n_s` and f in
`n_s = (120f)/(P)`

`850 = (120 * 60)/(P)`

`850 = (7200)/(P)`

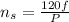
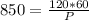
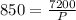
Multiply both sides by P

`P * 850 = (7200)/(P) * P`

`P * 850 = 7200`

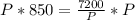
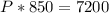
Divide both sides by 850

`(P * 850)/(850) = (7200)/(850)`

`P = (7200)/(850)`

`P = 8.47058823529`

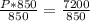
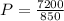
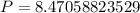
However, the number of poles must be an integer.

So:

`P = 8`