Question

If the spring constant is doubled, what value does the period have for a mass on a spring?

A. The period would double by square `sqrt(2)`.
B. The period would be halved by `sqrt(2)`.
C. The period would increase by `sqrt(2)`.
D. The period would decrease by `sqrt(2)`.

Please, explain your answer.

Answer 1

D. The period would decrease by `sqrt(2)`. is wrong on clever/plato

Step-by-step explanation:

i got it wrong :(

Answer 2

The period would decrease by `sqrt(2)`.

Explanation:

The angular frequency omega of an oscillating mass m due to a spring with a constant k is given by

`\omega = \sqrt{(k)/(m)}`

(this is obtained by solving the differential equation
`m\ddot{{ x}}-kx=0`)

If k doubles, i.e., k'=2k, then

`\omega'=\sqrt{(k')/(m)}=\sqrt{(2k)/(m)}=√(2)\sqrt{(k)/(m)}=\omega√(2)`

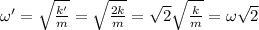
Since the angular frequency is
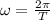`\omega = (2\pi)/(T)`, we can say that

`\omega√(2)=(2\pi)/(T)√(2)=(2\pi)/((T)/(√(2)))=(2\pi)/(T')`

and so it becomes clear that the period T will decrease by sqrt(2) as stated in choice (D).