Answer:
C. 5
Explanation:
We are given that the polygon has total 5 diagonals.
It is known that the formula for the number of diagonals in a polygon is,
Number of diagonals =
 , where n is the number of sides.
, where n is the number of sides.
As, the total number of diagonals in the given polygon are 5.
So, we get,
5 =

i.e.
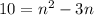
i.e.
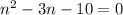
Since, the solution of a quadratic equation
 is given by,
is given by,
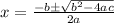
We have,
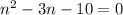 implies a= 1, b= -3 and c= -10.
implies a= 1, b= -3 and c= -10.
So, the solution is,
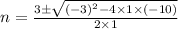
i.e.
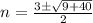
i.e.
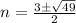
i.e.

i.e.
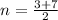 and i.e.
and i.e.
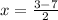
i.e.
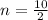 and i.e.
and i.e.
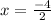
i.e. n= 5 and n= -2.
As, the number of sides cannot be negative.
So, n= 5.
Thus, the polygon will have 5 sides.