Answer:
The maximum speed of turn on the given circular track is 16.27 m/s.
Step-by-step explanation:
Given;
mass of the car, m = 2200 kg
radius of the track, r= 30 m
coefficient of static friction between the tires and the road, μ = 0.9
The net vertical force on the car = N = mg
The net horizontal force on the car = Centripetal force
The coefficient of static friction is given as;

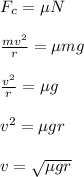
where;
v is the maximum speed of turn
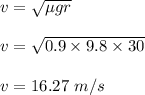
Therefore, the maximum speed of turn on the given circular track is 16.27 m/s.