Question

Sasha buys two ribbons of equal length. She cuts 9 pieces of the same length, L, from the first ribbon and finds that 5 inches are left over. She then cuts two pieces of the same length, L, from the second ribbon and finds that 40 inches are left over. What was the length of each ribbon when she bought them?

Answer 1

length of each ribbon was 50 inches.

Explanation:

We have been given that she cuts 9 pieces of the same length, L, from the first ribbon and finds that 5 inches are left over.

It means she had a total of 9L length of ribbon and if we add 5 to this, it should be equal to the original length of the ribbon when she bought.

If x be the length of the each ribbon when she bought them. It means if we add 5 to 9L then it should be equal to x.

`9L+5=x\\\\9L=x-5\\\\L=(1)/(9)(x-5)...(1)`

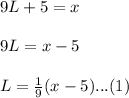
On the same way, we have the second equation as

`2L+40=x`

Plugging the value of L from equation 1, we get

`2\cdot((1)/(9)(x-5))+40=x\\\\(2)/(9)x-(10)/(9)+40=x=x\\\\(2)/(9)x+(350)/(9)=x\\\\(350)/(9)=x-(2)/(9)x\\\\(350)/(9)=(7x)/(9)\\\\x=50`

Hence, length of each ribbon was 50 inches.