Question

On the first day of baseball tournament Jessie scored 2 runs. On the second day, 4 runs. On the third day, 6 runs. If this pattern continues, how many runs should Jessie score on the eighth day?

Answer 1

16 runs on the eighth day; the pattern is to add two more every day

Explanation:

day 1: 2 runs

day 2: 4 runs

day 3: 6 runs

day 4: 8 runs

day 5: 10 runs

day 6: 12 runs

day 7: 14 runs

day 8: 16 runs

Answer 2

16 runs.

Explanation:

We have been given that on the first day of baseball tournament Jessie scored 2 runs. On the second day, 4 runs. On the third day, 6 runs.

We can see that runs scored by Jessie form an arithmetic sequence, where each successive term is 2 more than the previous term.

Since we know that formula for nth term of an arithmetic sequence is:
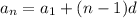`a_n=a_1+(n-1)d`, where,

`a_n=\text{nth term of the sequence}`,

`a_1=\text{1st term of the sequence}`,

`n=\text{Number of terms of the sequence}`,

`d=\text{Common difference}`.

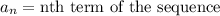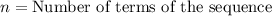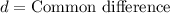Since on the first day Jessie scored 2 runs, so
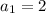`a_1=2` and difference between two consecutive terms is 2 (4-2=2), so d will be 2.

Upon substituting our values in arithmetic sequence formula we will get,

`a_n=2+(n-1)*2`

`a_n=2+2n-2`

`a_n=2n`

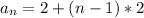
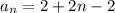
Therefore, formula for nth term of sequence representing number scored by Jessie on the baseball tournament is
`a_n=2n`.

Let us find the 8th term of sequence by substituting n=8 in our sequence formula.

`a_8=2*8`

`a_8=16`

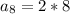
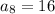
Therefore, Jessie should score 16 runs on the eighth day of baseball tournament.