Answer:
The value of x is 94 cm.
Explanation:
Given information: VT=95.2 cm, VY=34 cm, and TK=168 cm.
Let the length of YK be y.
Since TY is angle bisector, therefore by triangle angle bisector theorem we get
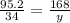
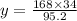
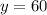
The length of YK is 60 cm.
The value of x is
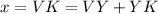
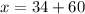
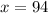
Therefore the value of x is 94 cm.