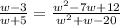Question

Change the fraction w-3/w+5 into an equivalent fraction with the denominator w2 + w – 20.

Answer 1

ANSWER


`\frac{ {w}^(2) - 7w + 12}{ {w}^(2) + w - 20 }`

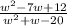
Step-by-step explanation


The given fraction is,


`(w - 3)/(w + 5)`

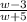
To get an equivalent fraction, we multiply both the numerator and the denominator by the same quantity that will give us

w²+w-20

in the denominator.


This implies that,


`(w - 3)/(w + 5) = ((w - 3)(w - 4))/((w + 5)(w - 4))`

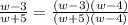
We multiply out the numerators and denominators using the distributive property to obtain,



`(w - 3)/(w + 5) = \frac{ {w}^(2) - 4w - 3w + 12}{ {w}^(2) - 4w + 5w - 20 }`

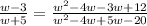
This simplifies to


`(w - 3)/(w + 5) = \frac{ {w}^(2) - 7w + 12}{ {w}^(2) + w - 20 }`