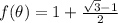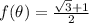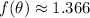Answer:
The approximate value of
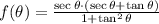 is 1.366.
is 1.366.
Explanation:
Let
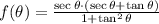 , we proceed to simplify the formula until a form based exclusively in sines and cosines is found. From Trigonometry, we shall use the following identities:
, we proceed to simplify the formula until a form based exclusively in sines and cosines is found. From Trigonometry, we shall use the following identities:
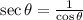 (1)
(1)
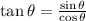 (2)
(2)
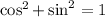 (3)
(3)
Then, we simplify the given formula:
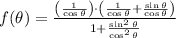
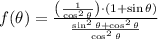
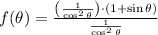
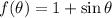
If we know that
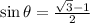 , then the approximate value of the given function is:
, then the approximate value of the given function is: