Question

A sphere is originally at a temperature of 500°c. The sphere is melted and recast, without loss of mass, into a cube with the same emissivity as the sphere. Calculate the Celsius temperature of the cube if it is to emit the same radiant powers the sphere​

Answer 1

Answer: The value of the celsius temperature of the cube is 472.2°c.

Explanation:

The expression for the power radiated is as follows;

`P=A\epsilon\sigma T^(4)`

Here, A is the area,
`\sigma` is the stefan's constant,
`\epsilon` is the emissivity and T is the temperature.

It is given in the problem that A sphere is originally at a temperature of 500°c. The sphere is melted and recast, without loss of mass, into a cube with the same emissivity as the sphere.

Then the expression for the radiated power for the cube and the sphere can be expressed as;

`A_(1)\epsilon \e\sigma T_(1)^(4)=A_(2)\epsilon \e\sigma T_(2)^(4)`

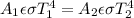
Here,
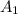`A_(1)` is the area of the sphere,
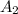`A_(2)` is the area of the cube,
`T_(1)` is the temperature of the sphere and
`T_(2)` is the temperature of the cube.

The radiated powers and emissivity of the cube and the sphere are same.

`A_(1)T_(1)^(4)=A_(2)T_(2)^(4)`

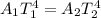
The area of the sphere is
`A_(1)=4\pi * r^(2)`.

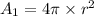Here, r is the radius of the sphere.

The area of the cube is
`A_(2)=6* a^(2)`.

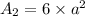Here, a is the edge of the cube.

Put
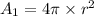`A_(1)=4\pi * r^(2)` and
`A_(2)=6* a^(2)`.

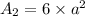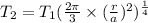`T_(2)=T_(1)((2\pi )/(3)* ((r)/(a))^(2))^{(1)/(4)}` ....(1)

The masses and the densities of the sphere and the cube are same. Then the volumes are also same.

`V_(1)=V_(2)`

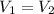
Here,
`V_(1),V_(1)` are the volumes of the sphere and the cube.

`(4)/(3)\pi r^(3)=a^(3)`

`(r)/(a)=((3)/(4\pi ))^{(1)/(3)}`

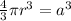
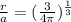
Put this value in the equation (1).

`T_(2)=T_(1)((2\pi )/(3)* ((r)/(a))^(2))^{(1)/(4)}`
`T_(2)=T_(1)((2\pi )/(3)* (((3)/(4\pi ))^{(1)/(3)})^(2))^{(1)/(4)}`

Put T_{1}=500°c.

`T_(2)=(500)((2\pi )/(3)* ((3)/(4\pi ))^{(2)/(3)})^{(1)/(4)}`

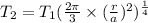
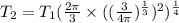
`T_(2)=472.2^(\circ)c`

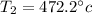
Therefore, the value of the celsius temperature of the cube is 472.7°c.