Question

Choose the function whose graph is given by:

Answer 1

The correct option is B.

Explanation:

From the given graph it is clear that the maximum value of the function is 2 at x=0, so it a cosine function.

The general form of a cosine function is

`y=a\cos(bx+c)+d` .... (1)

Where, a is amplitude, 2π/b is period, c is phase shift and d is midline.

Since maximum value is 2 and minimum value is 0, so

`Amplitude=a=(2-0)/(2)=1`

`Midline=b=(2+0)/(2)=1`

`Period=2\pi\Rightarrow b=1`

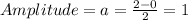
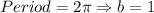
Since maximum value is at x=0, therefore the phase shift is c=0.

Put these values in equation 1.

`y=1\cos(1x+0)+1`

`y=\cos(x)+1`

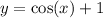
Therefore the correct option is B.

Answer 2

Option B. y = cosx + 1

Explanation:

To understand the given graph we will note down it's features as below.

1). Since it's a periodic function and y value of graph is maximum at x=0 so its a cosine function.

2). Vertical shift of the graph is 1 means y=0 is the mid line of the graph.

3). Amplitude of the graph is = (2-0)/2 = 1

4). Phase shift of the given graph = 0

The graph satisfying all properties is option B. y = cosx + 1