Question

Prove that the sum of two consecutive exponents of the number 6 is divisible by 7.

Answer 1

Explanation:

To prove: The sum of two consecutive exponents of the number 6 is divisible by 7.

Proof: Let the consecutive exponents of the number 6 be:

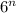`6^(n)` and
`6^(n+1)`.

Then , the sum of two consecutive exponents of the number 6 is represented as :

`6^(n)+6^(n+1)`.

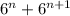Now, according to question, we have to prove that The sum of two consecutive exponents of the number 6 is divisible by 7, thus

`6^(n)+6^(n+1) =6^(n)+6^(n){*}6`

=
`6^(n)(1+6)`

⇒
`6^(n)+6^(n+1)`=
`6^(n)(7)`

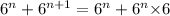
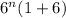
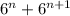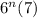
which means that the sum of two consecutive exponents of the number 6 is divisible by 7.

Hence proved.