Answer:
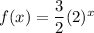
Explanation:
The given sequence is
{3, 6, 12, 24, 48, 96, ...}
It means f(x)=3, 6, 12, 24, 48, 96, ... for x=1,2,3,4,5,6,.. respectively.
We need to find non-linear function in the form
 ...(1)
...(1)
We know that f(x)=3 for x=1.
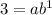 ....(i)
....(i)
We know that f(x)=6 for x=2.
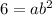 ....(ii)
....(ii)
Divide equation (ii) by (i).
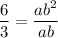

Substitute b=2 in equation (1).
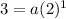
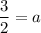
Substitute
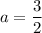 and
and
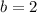 in (1).
in (1).
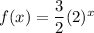
Therefore, the required function is
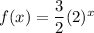 .
.