Question

The game commission observes the fish population in a stream and notices that the number of trout increases by a factor of 1.5 every week. The commission initially observed 80 trout in the stream.

a. Write the explicit formula for the trout situation. (+2)

b. Make and upload a graph of the population growth. (+2) Does the graph show a linear function or an exponential function? (+1) Explain. (+2)

c. If this pattern continues, how many trout will be in the stream on the fifth week? (+1)

d. If this pattern continues, on what week will the trout population exceed 500? Justify your reasoning. (+2)

Answer 1

A -
`f(t)=80(1.5)^t`

B - Graph given below

C - Number of trouts in 5th week are 607.2

D - Population of trouts will exceed 500 on the 5th week.

Explanation:

We are given that,

The number of trout increases by a factor of 1.5 each week and the initial population of the trout is observed to be 80.

Part A: So, the explicit formula representing the situation is,

`f(t)=80(1.5)^t`, where f(t) represents the population of trouts after 't' weeks.

Part B: The graph of the function can be seen below.

It can be seen that the function is an exponential function.

Part C: It is required to find the number of trouts in the 5th week.

So, we have,

`f(5)=80(1.5)^5`

i.e.
`f(5)=80* 7.59`

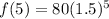
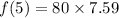
i.e. f(5) = 607.2

Thus, the number of trouts in 5th week are 607.2

Part D: We are given that the trout population exceeds 500.

It is required to find the week in which this happens.

So, we have,

`50<80(1.5)^t`

i.e.
`(1.5)^t>(500)/(80)`

i.e.
`(1.5)^t>6.25`

i.e.
`t\log 1.5>\log 6.25`

i.e.
`t* 0.1761>0.7959`

i.e.
`t>(0.7959)/(0.1761)`

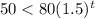
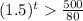
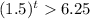
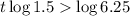
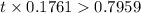
i.e. t > 4.5

As, t represents the number of weeks. So, to nearest whole, t = 5.

Thus, the population of trouts will exceed 500 on the 5th week.