Answer:
The keys landed 8.11 feet from the base of the tower.
Explanation:
Let after landing on the ground x be the distance of keys from the base of the tower,
Given, the height of the tower = 65.6 feet,
And, it leans to the left at 7.1 degrees,
So, the angle made by tower to the vertical line = 71°
Thus, by making the diagram of the given situation,
We can write,
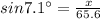 (
(
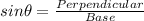 )
)

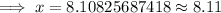
Hence, the keys landed 8.11 feet from the base of the tower.