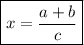Question

Solve the following equation for x (linear equation):


`(b-cx)/(a) + (a-cx)/(b) + 2 = 0`

Answer 1

`\displaystyle x=(a+b)/(c)`

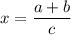
Explanation:

Equations

Solve the equation:

`\displaystyle (b-cx)/(a)+(a-cx)/(b)+2=0`

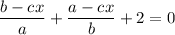
Subtracting 2:

`\displaystyle (b-cx)/(a)+(a-cx)/(b)=-2`

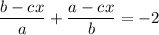
Multiply by ab to eliminate denominators:

`\displaystyle ab(b-cx)/(a)+ab(a-cx)/(b)=-2ab`

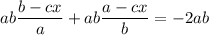
Simplifying:

`b(b-cx)+a(a-cx)=-2ab`

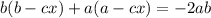
Operating:

`b^2-bcx+a^2-acx=-2ab`

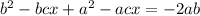
Subtracting
`b^2+a^2`

`-bcx-acx=-2ab-b^2-a^2`

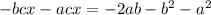
Multiplying by -1:

`bcx+acx=2ab+b^2+a^2`

Factoring:

`c(b+a)x=2ab-b^2+a^2`

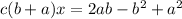
The right side of the equation is the square of a+b:

`c(b+a)x=(a+b)^2`

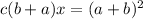
Simplifying (for a ≠ -b):

`cx=(a+b)`

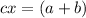
Dividing by c:

`\boxed{\displaystyle x=(a+b)/(c)}`