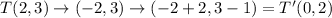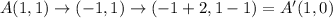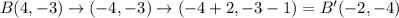Question

Perform the following transformations in the pictures below.

Answer 1

I’m not sure, sorry!

Answer 2

QUESTION A

ΔALT has coordinates
`A(-5,-1),L(-3,-2),T(-3,2)`.

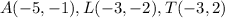If we translate by the rule
`(x,y)\rightarrow (x+6,y-3)`

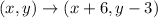
Then;

`A(-5,-1)\rightarrow (-5+6,-1-3)=(1,-4)`.

`B(-3,-2)\rightarrow (-3+6,-2-3)=(3,-5)`.

`T(-3,2)\rightarrow (-3+6,2-3)=(3,-1)`.

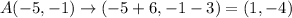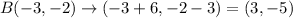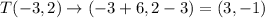A reflection over the y-axis has the mapping

`(x,y)\rightarrow (-x,y)`

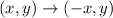
If we reflect the resulting points over the y-axis, we obtain,

`A(-5,-1)\rightarrow (1,-4)\rightarrow A'(-1,-4)`.

`B(-3,-2)\rightarrow (3,-5)\rightarrow B'(-3,-5)`.

`T(-3,2)\rightarrow (3,-1)\rightarrow C'(-3,-1)`.

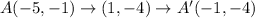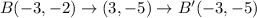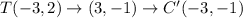QUESTION B

ΔTAB has vertices
`T(2,3),A(1,1),B(4,-3)`.

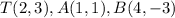A reflection over the x-axis has the mapping

`(x,y)\rightarrow (x,-y)`

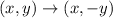
A reflection over the y-axis also has the mapping;

`(x,y)\rightarrow (-x,y)`

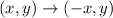
If we reflect ΔTAB over the x-axis and reflect the resulting image over the y-axis, we obtain;

`T(2,3)\rightarrow (2,-3) \rightarrow T'(-2,-3)`

`A(1,1)\rightarrow (1,-1) \rightarrow A'(-1,-1)`

`B(4,-3)\rightarrow (4,3) \rightarrow B'(-4,3)`

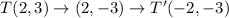
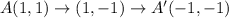
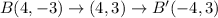
QUESTION C

ΔALT has vertices
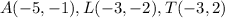`A(-5,-1),L(-3,-2),T(-3,2)`.

A
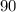`90\degree` clockwise rotation about the origin has the mapping;

`(x,y)\rightarrow (y,-x)`

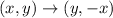
A reflection in the line y=x also has the mapping;

`(x,y)\rightarrow (y,x)`

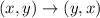
When we rotate the given triangle
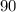`90\degree` clockwise about the origin, and then reflect the image over the line y=x, we obtain;

`A(-5,-1)\rightarrow (-1,5)\rightarrow A'(5,-1)`

`L(-3,-2)\rightarrow (-2,3)\rightarrow L'(3,-2)`

`T(-3,2)\rightarrow (2,3)\rightarrow T'(3,2)`

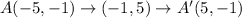
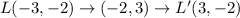
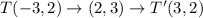
QUESTION D

ΔTAB has vertices
`T(2,3),A(1,1),B(4,-3)`.

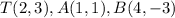A reflection over the y-axis has the mapping;

`(x,y)\rightarrow (-x,y)`

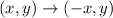
The rule for the given translation is

`(x,y)\rightarrow (x+2,y-1)`

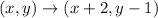
If reflect the given triangle over the y-axis and translate using the rule
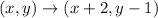`(x,y)\rightarrow (x+2,y-1)`, we obtain;

`T(2,3)\rightarrow (-2,3)\rightarrow (-2+2,3-1)=T'(0,2)`

`A(1,1)\rightarrow (-1,1)\rightarrow (-1+2,1-1)=A'(1,0)`

`B(4,-3)\rightarrow (-4,-3)\rightarrow (-4+2,-3-1)=B'(-2,-4)`