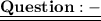
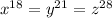
3,
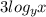 ,
,
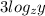 and
and
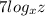 are in??
are in??
The Series in AP.
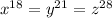

By taking LOG on both sides

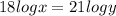
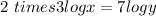
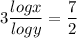
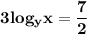
Now,

By taking LOG on both sides
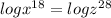
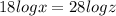
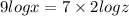
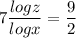
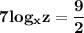
Now,
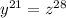
By taking LOG on both sides
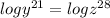

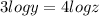
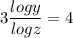
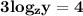
According to the question:-
3,
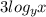 ,
,
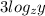 and
and
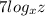 are ...in??
are ...in??
we have,
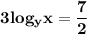
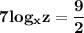
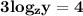
The series is,
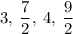
Here,

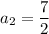

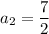
Let, us find common difference
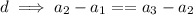
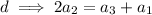
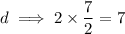
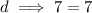
Since, common difference is equal!
The series is in AP.