Question

Complete the similarity statement for the two triangles shown. Enter your answer in the box. △XBR∼△ Two similar triangles B R X and N J Y. In triangle B R X, side B X is the base. Side B R is labeled 30 centimeters, side R X is labeled 40 centimeters, and side B X is labeled 60 centimeters. In triangle N J Y, side N Y is the base. Side N J is labeled 15 centimeters, side J Y is labeled 20 centimeters, and side N Y is labeled 30 centimeters. The measure of angle B equals the measure of angle N, the measure of angle R equals the measure of angle J, and the measure of angle X equals the measure of angle Y.

Answer 1

YNJ

Explanation:

Answer 2

Here, BRX and NJY are two triangles in which,

BR = 30 cm, RX = 40 cm, BX = 60 cm, NJ = 15 cm, JY = 20 cm and NY = 30 cm,

Also, m∠B = m∠N, m∠R = m∠J and m∠X = m∠Y,

By the property of congruence,

`\angle B \cong \angle N`,
`\angle R \cong \angle J` and
`\angle X \cong \angle Y`

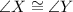
Thus, By AAA similarity postulate,

`\triangle BRX\sim \triangle NJY`

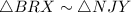
Hence, proved.