Question

PLEASE HELP ME. I NEED YOUR HELP ASAP PLEASEEE.

Select ALL the correct answers.
In a experiment, it was found that the population of a bacterial colony doubles every 10 minutes. The following function represents the number of bacteria in the colony after x minutes.

Which statements are true?

Answer 1

Options A and B.

Explanation:

The general exponential growth function is

`g(x)=a(1+r)^x`

where, a is the initial value, r is rate of change, x is time.

Consider the given function is

`f(x)=3(2)^{(x)/(10)}` ... (1)

here, function f(x) represents the number of bacteria in the colony after x minutes.

The given function can be rewritten as

`f(x)=3(1+1)^{(x)/(10)}` .... (2)

On comparing (1) and (2) we get

`r=1`

It means expression
`(2)^{(x)/(10)}` reveals that the population of the bacterial colony increases by 100% every 10 minutes.

Using the property of exponent, the given function can be written as

`f(x)=3(2^{(1)/(10)})^x`
`[\because a^(mn)=(a^m)^n]`

`f(x)\approx 3(1.07)^x`

It means expression
`(1.07)^x` reveals that the approximate rate of increase in the population of the bacterial colony per minute.

Therefore, the correct options are A and B.

Answer 2

Options A and B are true

Explanation:

In this question it is given that population of a bacterial colony doubles every 10 minutes and the function that represents the number of bacteria in colony after x minutes is
`3.(2)^{(x)/(10) }`

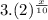
Now we check each option given

A. The expression
`(2)^{(x)/(10) }` reveals the population of the bacterial colony increases by 100% every 10 minutes.

Let's check by putting x = 10

`3.(2)^{(10)/(10)}=(3).(2) = 6`

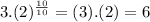
Here after 10 minutes initial population which was 3 got doubled to 6. So option A is true.

B. Expression
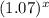`(1.07)^(x)` reveals the approximate rate of increase in the population of the bacterial colony per minute.

Let's solve the expression

`3.(2)^{(x)/(10)}=3.[(2)^{(1)/(10)}]^(x)=3.[1.07]^(x)`

Option B is true.

C. This option is not correct as we have already solved the expression in option B.

D. This option can't be correct because it is itself given in the question that
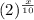`(2)^{(x)/(10)}` reveals that the bacterial colony increases by 100% in 10 minutes.

E. Let's check this option by putting x = 1 minute in
`3.(2)^{(x)/(10) }`

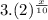
and in
`(1024)^(x)` . If solutions of both the expressions are same then this option will be correct.

`3.(2)^{(x)/(10) }=3.(2)(1)/(10)=3.(1.07)=3.21`

And
`(1024)^(x)=(1024)^(1)=1024`

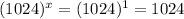
As both the solutions are different so Option E is incorrect.

F. As we have seen in option E both the expressions give different values for different values of x so Option F will be incorrect again.

Options A and B are true.