Question

In the diagram below de and ef are tangent to o what is the measure of E

Answer 1

Answer: 32

Step-by-step expanation:

Answer 2

Option D is correct

`\angle E = 32^(\circ)`

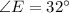
Explanation:

In the given diagram below DE and EF are tangent to O.

Join the point D and O and O and F as shown below.

It is given that:

`\text{arc(DF)} = \angle DOF`

⇒
`148^(\circ) = \angle DOF`

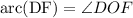
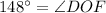
or

`\angle DOF = 148^(\circ)`

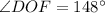
A line is tangent to circle if and only if the line is perpendicular to the radius drawn to the point of tangency.

Since, DE and EF are tangent

then:

`\angle ODE = \angle OFE = 90^(\circ)`

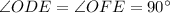
In a quadrilateral EDOF:

Sum of all the angles add up to 360 degree.

`\angle FED +\angle ODE + \angle DOF+ \angle OFE = 360^(\circ)`

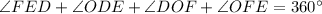
Substitute the given values we have;

`\angle FED +90^(\circ)+ 148^(\circ) +90^(\circ) = 360^(\circ)`

⇒
`\angle FED + 328^(\circ) = 360^(\circ)`

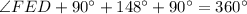
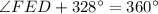
Subtract 328 degree from both sides we have;

`\angle FED = 32^(\circ)`

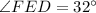
Therefore, the measure of angle E is, 32 degree.