Answer:
Option 2 is correct that is area of triangle is 7 m².
Explanation:
Given: Equilateral Triangle is given.
Semi Perimeter of triangle = 6
To find: Area of the triangle
Let, Side of equilateral triangle be x
Semi Perimeter, s =
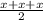
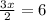
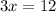

By Heron's formula,
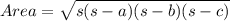

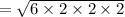
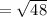

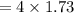
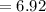
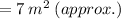
Therefore, Option 2 is correct that is area of triangle is 7 m².