Question

How do you solve these equations? I don't want you to answer all of them, just tell me how to solve each type of equation on the sheet.​

Answer 1

8. Identify the common denominator; express each fraction using that denominator; combine the numerators of those rewritten fractions and express the result over the common denominator. Factor out any common factors from numerator and denominator in your result. (It's exactly the same set of instructions that apply for completely numerical fractions.)

9. As with numerical fractions, multiply the numerator by the inverse of the denominator; cancel common factors from numerator and denominator.

10. The method often recommended is to multiply the equation by a common denominator to eliminate the fractions. Then solve in the usual way. Check all answers. If one of the answers makes your multiplier (common denominator) be zero, it is extraneous. (10a cannot have extraneous solutions; 10b might)

Explanation:

For a couple of these, it is helpful to remember that (a-b) = -(b-a).

8d.

`(5)/(x+2)+(25-x)/(x^2-3x-10)=(5(x-5))/((x+2)(x-5))+(25-x)/((x+2)(x-5))\\\\=(5x-25+25-x)/((x+2)(x-5))=(4x)/(x^2-3x-10)`

___

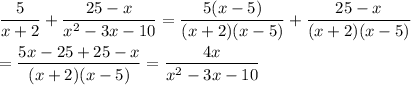
9b.

`\displaystyle(\left((x)/(x-2)\right))/(\left((2x)/(2-x)\right))=(x)/(x-2)\cdot(-(x-2))/(2x)=(-x(x-2))/(2x(x-2))=-(1)/(2)`

___

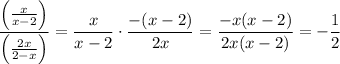
10b.

`(3)/(x-1)+(6)/(x^2-3x+2)=2\\\\(3(x-2))/((x-1)(x-2))+(6)/((x-1)(x-2))=(2(x-1)(x-2))/((x-1)(x-2))\\\\3x-6+6=2(x^2-3x+2) \qquad\text{multiply by the denominator}\\\\2x^2-9x+4=0 \qquad\text{subtract 3x}\\\\(2x-1)(x-4)=0 \qquad\text{factor; x=1/2, x=4}`

Neither solution makes any denominator be zero, so both are good solutions.