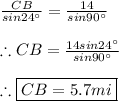Question

Solving right triangles

Answer 1

1. Answer:

A right triangles is a triangle having a 90 degree side. According to the figure, the sides of this triangle are expressed in inches. Therefore, we can find the missing sides and angles as follows:

m∠B:

The sum of the three interior angles of any triangle is 180°, therefore:

`m \angle B + 51^(\circ) + 90^(\circ) = 180^(\circ) \\ \\ \boxed{m \angle B = 39^(\circ)}`

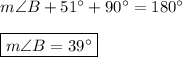
CA and AB:

We must use the law of sines as follows:

`(CA)/(sin39^(\circ))=(9)/(sin51^(\circ)) \\ \\ \therefore CA=(9sin39^(\circ))/(sin51^(\circ)) \\ \\ \therefore \boxed{CA=7.3in}`

`(AB)/(sin90^(\circ))=(9)/(sin51^(\circ)) \\ \\ \therefore AB=(9sin90^(\circ))/(sin51^(\circ)) \\ \\ \therefore \boxed{AB=11.6in}`

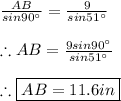
2. Answer:

According to the figure, the sides of this triangle are expressed in meters. Therefore, we can find the missing sides and angles as follows:

m∠A:

The sum of the three interior angles of any triangle is 180°, therefore:

`m \angle A + 53^(\circ) + 90^(\circ) = 180^(\circ) \\ \\ \boxed{m \angle A = 37^(\circ)}`

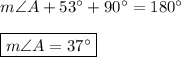
CA and CB:

We must use the law of sines as follows:

`(CA)/(sin53^(\circ))=(5)/(sin90^(\circ)) \\ \\ \therefore CA=(5sin53^(\circ))/(sin90^(\circ)) \\ \\ \therefore \boxed{CA=4.0m}`

`(CB)/(sin37^(\circ))=(5)/(sin90^(\circ)) \\ \\ \therefore CB=(5sin37^(\circ))/(sin90^(\circ)) \\ \\ \therefore \boxed{CB=3.0m}`

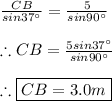
3. Answer:

According to the figure, the sides of this triangle are expressed in miles. Therefore, we can find the missing sides and angles as follows:

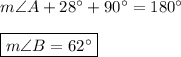
m∠B:

The sum of the three interior angles of any triangle is 180°, therefore:

`m \angle A + 28^(\circ) + 90^(\circ) = 180^(\circ) \\ \\ \boxed{m \angle B = 62^(\circ)}`

CB and AB:

We must use the law of sines as follows:

`(CB)/(sin28^(\circ))=(29.3)/(sin62^(\circ)) \\ \\ \therefore CB=(29.3sin28^(\circ))/(sin62^(\circ)) \\ \\ \therefore \boxed{CA=15.6mi}`

`(AB)/(sin90^(\circ))=(29.3)/(sin62^(\circ)) \\ \\ \therefore AB=(29.3sin90^(\circ))/(sin62^(\circ)) \\ \\ \therefore \boxed{AB=33.2mi}`

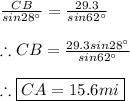
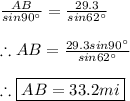
4. Answer:

According to the figure, the sides of this triangle are expressed in miles. Therefore, we can find the missing sides and angles as follows:

m∠A:

The sum of the three interior angles of any triangle is 180°, therefore:

`m \angle A + 24^(\circ) + 90^(\circ) = 180^(\circ) \\ \\ \boxed{m \angle A = 66^(\circ)}`

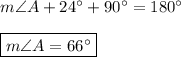
CA and CB:

We must use the law of sines as follows:

`(CA)/(sin66^(\circ))=(14)/(sin90^(\circ)) \\ \\ \therefore CA=(14sin66^(\circ))/(sin90^(\circ)) \\ \\ \therefore \boxed{CA=12.8mi}`

`(CB)/(sin24^(\circ))=(14)/(sin90^(\circ)) \\ \\ \therefore CB=(14sin24^(\circ))/(sin90^(\circ)) \\ \\ \therefore \boxed{CB=5.7mi}`