Question

If 12 is replaced with 3 in the following set, what will happen to the value of the interquartile range? 28, 45, 12, 34, 36, 45, 19, 20 It will increase. It will decrease. It will stay the same.

Answer 1

It will stay same.

Explanation:

The given data is:

28, 45, 12, 34, 36, 45, 19, 20.

In order to find the interquartile range, first arrange them given data in ascending order, we get

12,19 ,20, 28, 34, 36, 45, 45.

Now, calculate the median of the above data, we get

Median=
`(28+34)/(2)=(62)/(2)=31`

Now, find the median of the upper and the lower half.

Median of Upper half:
`(36+45)/(2)=(81)/(2)` and

Median of lower half:
`(19+20)/(2)=(39)/(2)`

The interquartile range of this data is : Median of Upper half- median of lower half=
`(81)/(2)-(39)/(2)=21`.

Now, if we replace 12 with 3 in the given data, we get

3, 19 ,20, 28, 34, 36, 45, 45 in ascending order.

Now, calculate the median of the above data, we get

Median=
`(28+34)/(2)=(62)/(2)=31`

Now, find the median of the upper and the lower half.

Median of Upper half:
`(36+45)/(2)=(81)/(2)` and

Median of lower half:
`(19+20)/(2)=(39)/(2)`

The interquartile range of this data is : Median of Upper half- median of lower half=
`(81)/(2)-(39)/(2)=21`.

Itcan be seen that the interquartile range remains the same even after replacing 12 with 3.

Therefore, the interquartile range will remain the same.

Answer 2

The interquartile range remains the same.

Explanation:

Interquartile range is the difference between first and third quartile.

`I.Q.R.=Q_3-Q_1`

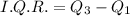
The given data is

28, 45, 12, 34, 36, 45, 19, 20

Arrange the data is ascending order.

12, 19, 20, 28, 34, 36, 45, 45

(12, 19, 20, 28), (34, 36, 45, 45)

(12, 19), (20, 28), (34, 36), (45, 45)

The first quartile is midpoint of 19 and 20 and the third quartile is the midpoint of 36 and 45.

`Q_1=(19+20)/(2)=19.5`

`Q_3=(36+45)/(2)=40.5`

`I.Q.R.=Q_3-Q_1`

`I.Q.R.=40.5-19.5=21`

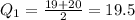
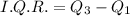
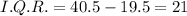
The interquartile range of given data is 21.

If 12 is replaced with 3 in the following set, then the given data is

3, 19, 20, 28, 34, 36, 45, 45

(3, 19, 20, 28), (34, 36, 45, 45)

(3, 19), (20, 28), (34, 36), (45, 45)

The first quartile is midpoint of 19 and 20 and the third quartile is the midpoint of 36 and 45.

`Q_1=(19+20)/(2)=19.5`

`Q_3=(36+45)/(2)=40.5`

`I.Q.R.=Q_3-Q_1`

`I.Q.R.=40.5-19.5=21`

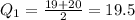
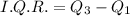
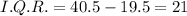
The interquartile range of given data is 21.

The interquartile range remains the same. Therfore option 3 is correct.