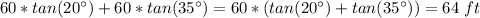Answer:
The height of the taller building is
Explanation:
see the attached figure to better understand the problem
step 1
Find the value of h1
with the angle of elevation
we know that
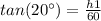
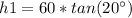
step 2
Find the value of h2
with the angle of depression
we know that
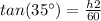
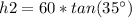
step 3
Find the height of the taller building
The height of the taller building is the sum of h1 plus h2
so