Question

A polygon with an area of (4x2 + 2x - 16) square units is combined with a rectangle that has a width of (6x + 2) units and a length of (x - 5) units. Then, a polygon with an area of (2x2 - 30x - 10) square units is removed. What is the area of the final polygon?

Answer 1

the Answer should be :

328

Answer 2

The area of new polygon is
`22 x^2 + 4 x - 16`.

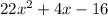Explanation:

The area of square =
`4x^2 + 2x - 16`

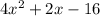
Width of the rectangle = 6x+2

Length of the rectangle = x-5

Area of the rectangle =
`(6x+2)(x-5)=6 x^2 - 28 x - 10`

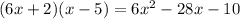
Then we combined square and rectangle. The area of combined figure is the sum of area of square and rectangle.

`\text{Combined area}=(4x^2 + 2x - 16)+(6 x^2 - 28 x - 10)`

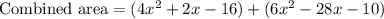
On combining like terms we get

`\text{Combined area}=(4x^2+6x^2)+ (2x-28x)+ (- 16- 10)`

`\text{Combined area}=10x^2-26x-26`

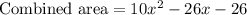
Then, a polygon with an area of
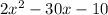`2x^2 - 30x - 10` square units is removed. So, new area of the polygon is

`Area=(10x^2-26x-26)-(2x^2 - 30x - 10)`

`Area=(10x^202x^2)+(-26x+30x)+(-26+10)`

`Area=8 x^2 + 4 x - 16`

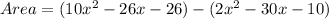
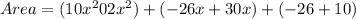
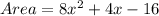
Therefore the area of new polygon is
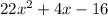`22 x^2 + 4 x - 16`.