Question

Which equation of the least squares regression line most closely matches the data set?

Note: The variable x represents the years after 1990.

 

Data set below

x y

1990 45

1992 51

1994 57

1996 61

1998 75


1. y=5.5x+52


2. y=2.2x+13.8


3. y=3.5x+43.8


4. y=3.5x−43.8

Answer 1

Answer: y = 3.5 x+ 43.8

Explanation:

Here x represents the number of years after 1990

Thus, we get the table that is used to find the equation will be,

x 0 2 4 6 8

y 45 51 57 61 75

Let the equation that shows the above data,

y = b + a x ---------(1)

`\text{Where, }a=(\sum y \sum x^2-\sum x \sum xy)/(n(\sum x^2)-(\sum x)^2)`

`\text{And, }b = (\sum xy - \sum x\sum y)/(n\sum x^2 - (\sum x)^2)`

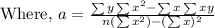
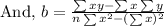
By the above table,

`\sum x = 20`

`\sum xy = 1296`

`\sum x^2 = 120`

`\sum y = 289`

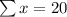
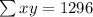
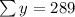
By substituting these values in the above value of a and b,

We get b = 43.8 and a = 3.5

Substitute this value in equation (1)

we get, the equation that shows the given data is,

y = 3.5 x + 43.8

⇒ Option (3) is correct.