Answer:
The solution of the given system of equations is (-6.667,7.667).
Explanation:
The given equations are
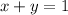 ...(1)
...(1)
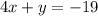 ....(2)
....(2)
put x=0 to find the y-intercept.
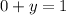
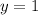
Therefore y-intercept of equation (1) is (0,1).

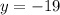
Therefore y-intercept of equation (2) is (0,-19).
put y=0 to find the y-intercept.
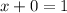

Therefore x-intercept of equation (1) is (1,0).
put y=0 to find the y-intercept.
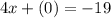

Therefore x-intercept of equation (1) is (-4.75,0).
Draw the graph of both lines by joining their x and y-intercept.
From the graph it is noticed that both the line intersect each other at (-6.667,7.667).
Therefore solution of the given system of equations is (-6.667,7.667).