Answer:
See the answers below.
Step-by-step explanation:
The magnitude can be easily found by means of the Pythagorean theorem.
![C = \sqrt{(C_(x))^(2) +(C_(y))^(2)} \\C=\sqrt{(105)^(2) +(88.2)^(2) } \\C=√(18804.24)\\C = 137.13 [m]](https://img.qammunity.org/2022/formulas/physics/high-school/2uhp6clzvc1l51f5bmnfgnckymz5gzp1mc.png)
We know that the coordinates in x and in y are negative, therefore the vector should be located in the fourth quadrant, see attached image.
And the angle with respect to the horizontal can be determined by means of the tangent of the angle.
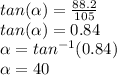
These are 40 degrees below the X-positive horizontal axis.