Answer: The answer is given below.
Step-by-step explanation: We are given an equality involving logarithm and we are to show the implication of L.H.S. to R.H.S.
We will be using the following two properties of logarithm:
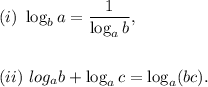
The proof is as follows:

Hence proved.