Answer:
see explanation
Explanation:
ΔABC is isosceles and AM is the perpendicular bisector to BC, hence
BM = MC = 4 cm
Using Pythagoras' identity on ΔABM, then
AB² = AM² + BM², that is
7² = AM² + 4²
49 = AM² + 16 ( subtract 16 from both sides )
33 = AM² ( take the square root of both sides )
AM =
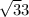
The area (A) of ΔABC is found using
A =
 bh ( b is the base BC and h the height AM )
bh ( b is the base BC and h the height AM )
A =
 × 8 ×
× 8 ×
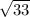 = 4
= 4
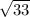 cm² ≈ 23 cm²
cm² ≈ 23 cm²