Question

Pls Help. Need ASAP. Calculus question.

Answer 1

`\displaystyle (sin(√(x)))/(4x)`

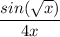
General Formulas and Concepts:

Algebra I

• Exponential Rule [Rewrite]:
  `\displaystyle b^(-m) = (1)/(b^m)`
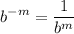
• Exponential Rule [Root Rewrite]:
  `\displaystyle \sqrt[n]{x} = x^{(1)/(n)}`

Calculus

Derivatives

Derivative Notation

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Integrals

Integration Rule [Fundamental Theorem of Calculus 2]:
`\displaystyle (d)/(dx)[\int\limits^x_a {f(t)} \, dt] = f(x)`

Explanation:

Step 1: Define

Identify

`\displaystyle g(t) = \int\limits^(√(x))_1 {(sin(t))/(2t)} \, dt`

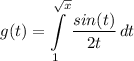
Step 2: Differentiate

1. Fundamental Theorem of Calculus 2 [Derivative Rule - Chain Rule]:
   `\displaystyle g'(x) = (sin(√(x)))/(2√(x)) \cdot (d)/(dx)[√(x)]`
2. Rewrite [Exponential Rule - Root Rewrite]:
   `\displaystyle g'(x) = (sin(√(x)))/(2√(x)) \cdot (d)/(dx) \bigg[ x^\bigg{(1)/(2)} \bigg]`
3. Basic Power Rule:
   `\displaystyle g'(x) = (sin(√(x)))/(2√(x)) \cdot (1)/(2)x^\bigg{(1)/(2) - 1}`
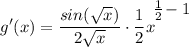
4. Simplify [Exponential Rule - Rewrite]:
   `\displaystyle g'(x) = (sin(√(x)))/(2√(x)) \cdot \frac{1}{2x^\bigg{(1)/(2)}}`
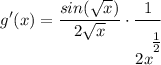
5. Rewrite [Exponential Rule - Root Rewrite]:
   `\displaystyle g'(x) = (sin(√(x)))/(2√(x)) \cdot (1)/(2√(x))`
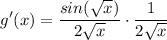
6. Multiply:
   `\displaystyle g'(x) = (sin(√(x)))/(4x)`

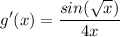
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Book: College Calculus 10e