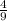Question

32-162k^2=0

Solve the equation by factoring. Check solutions.

Answer 1

see explanation

Explanation:

given 32 - 162k² = 0 ( factor out 2 from each term )

2(16 - 81k²) = 0

16 - 81k² ← is a difference of squares and factors in general as

• a² - b² = (a - b)(a + b)

16 = 4² ⇒ a = 4

81k² =(9k)² ⇒ b = 9k

16 - 81k² = (4 - 9k)(4 + 9k), thus

32 - 162k² = 0

2(4 - 9k)(4 + 9k) = 0

Equate each factor to zero and solve for k

4 - 9k = 0 ⇒ k =
`(4)/(9)`

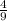
4 + 9k = 0 ⇒ k = -
`(4)/(9)`

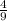
As a check

Substitute these values into the original equation and if left side equals right side then these are the solutions.

32 - 162 × ( -
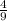`(4)/(9)`)² = 32 - 162 ×
`(16)/(81)` = 32 - 32 = 0

32 - 162 × (
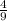`(4)/(9)`)² = 32 - 32 = 0

Hence solutions are k = ±
`(4)/(9)`